PSTAT 100: Lecture 13

Examples of Statistical Modeling

Ethan P. Marzban

Department of Statistics and Applied Probability; UCSB

Summer Session A, 2025

\[ \newcommand\R{\mathbb{R}} \newcommand{\N}{\mathbb{N}} \newcommand{\E}{\mathbb{E}} \newcommand{\Prob}{\mathbb{P}} \newcommand{\F}{\mathcal{F}} \newcommand{\1}{1\!\!1} \newcommand{\comp}[1]{#1^{\complement}} \newcommand{\Var}{\mathrm{Var}} \newcommand{\SD}{\mathrm{SD}} \newcommand{\vect}[1]{\vec{\boldsymbol{#1}}} \newcommand{\Cov}{\mathrm{Cov}} \DeclareMathOperator*{\argmin}{\mathrm{arg} \ \min} \]

Recap

• We can think of a model as a mathematical or idealized representation of a system.

• In statistical modeling, we adopt a three-step procedure:

  1. Propose a model
  2. Fit the model to the data
  3. Assess how well we believe our model is performing.

• There are two main types of statistical models: parametric and nonparametric.

  • The model fitting step differs between these types of models.

• Today, let’s explore two examples of modeling: one nonparametric, and one parametric.

Nonparametric Modeling: An Example

Density Estimation

Density Estimation

Framework

• Data: A collection of numerical values; \(\vect{x} = (x_1, \cdots, x_n)\) we believe to be a realization of an i.i.d. random sample \(\vect{X} = (X_1, \cdots, X_n)\) taken from a distribution with density f().

• Goal: to estimate the true value of f() at each point.

data.frame(samp) %>% ggplot(aes(x = samp)) +
  geom_histogram(aes(y = after_stat(density)), bins = 15, col = "white") +
  theme_minimal(base_size = 18) +
  ggtitle("Histogram of Sample Values") + xlab("value")

Density Estimation

Histograms

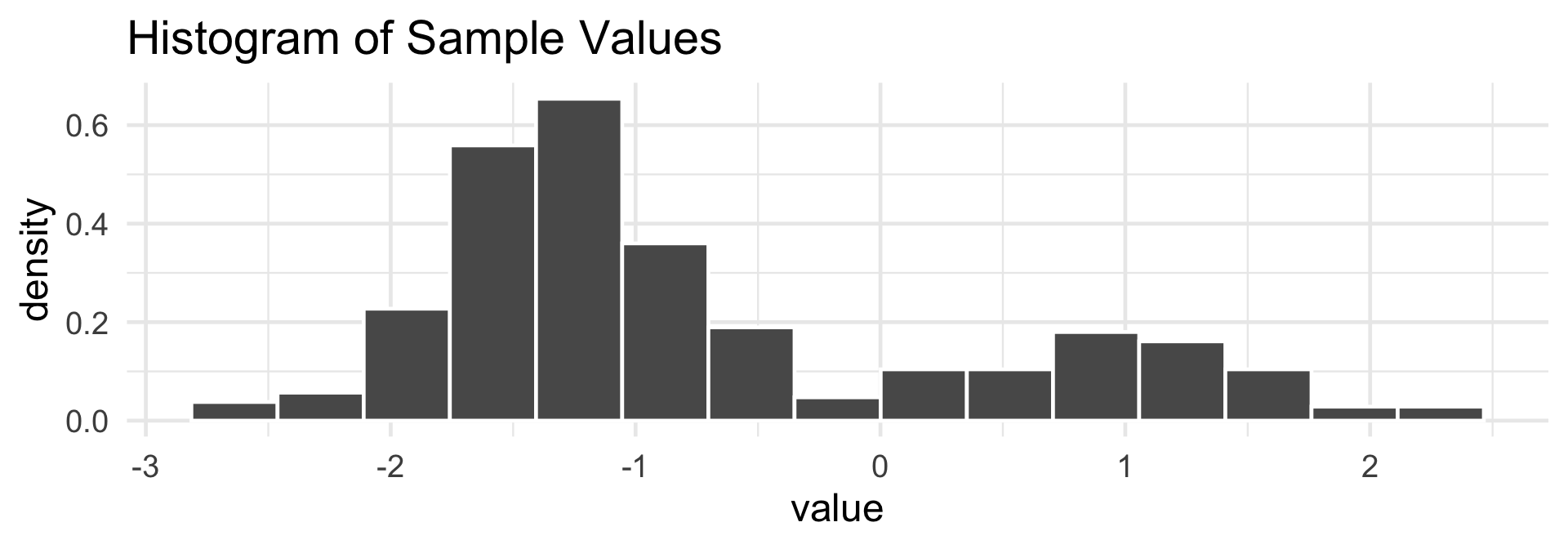
• Believe it or not, a histogram is actually a nonparametric attempt at modeling precisely this situation!

Important

There are actually two kinds of histograms: frequency histograms and density histograms.

• Frequency histograms are the ones we talked about in Week 1.
  • Density histograms take frequency histograms and rescale the y-axis so that the total area under the histogram is 1.
• Essentially, our “guess” for the value of the density at a given point x_i is simply the height of the density histogram at that point.

Histograms, Revisited

• If we let B_j denote the j^th bin, and if we have n observations, the height of the j^th bar on a density histogram is given by \[ \mathrm{height}_j = \frac{1}{nh} \sum_{i=1}^{n} 1 \! \! 1_{\{x_i \in B_j\}} \]

• Recall that the sum of indicators is a succinct way of writing “the number of observations that satisfy a condition”.

  • In this way, you should be able to interpret what the equation above is saying.
  • Perhaps an example may help:

Histograms, Revisited

Histograms, Revisited

• Given a new observation x, we can think of our “best guess” at the value of f(x) to be the height of the density histogram at x:

\[ \widehat{f}(x) = \frac{1}{nh} \sum_{i=1}^{n} \sum_{j} 1 \! \! 1_{\{x \in B_j\}} 1 \! \! 1_{\{x_i \in B_j\}} \]

• In other words, our estimate takes the input x, finds the bin to which x belongs, and returns the height of that bin.

• We call this procedure fixed binning, since, for a given x, we simply identify which, out of a set of fixed bins, x belongs to.

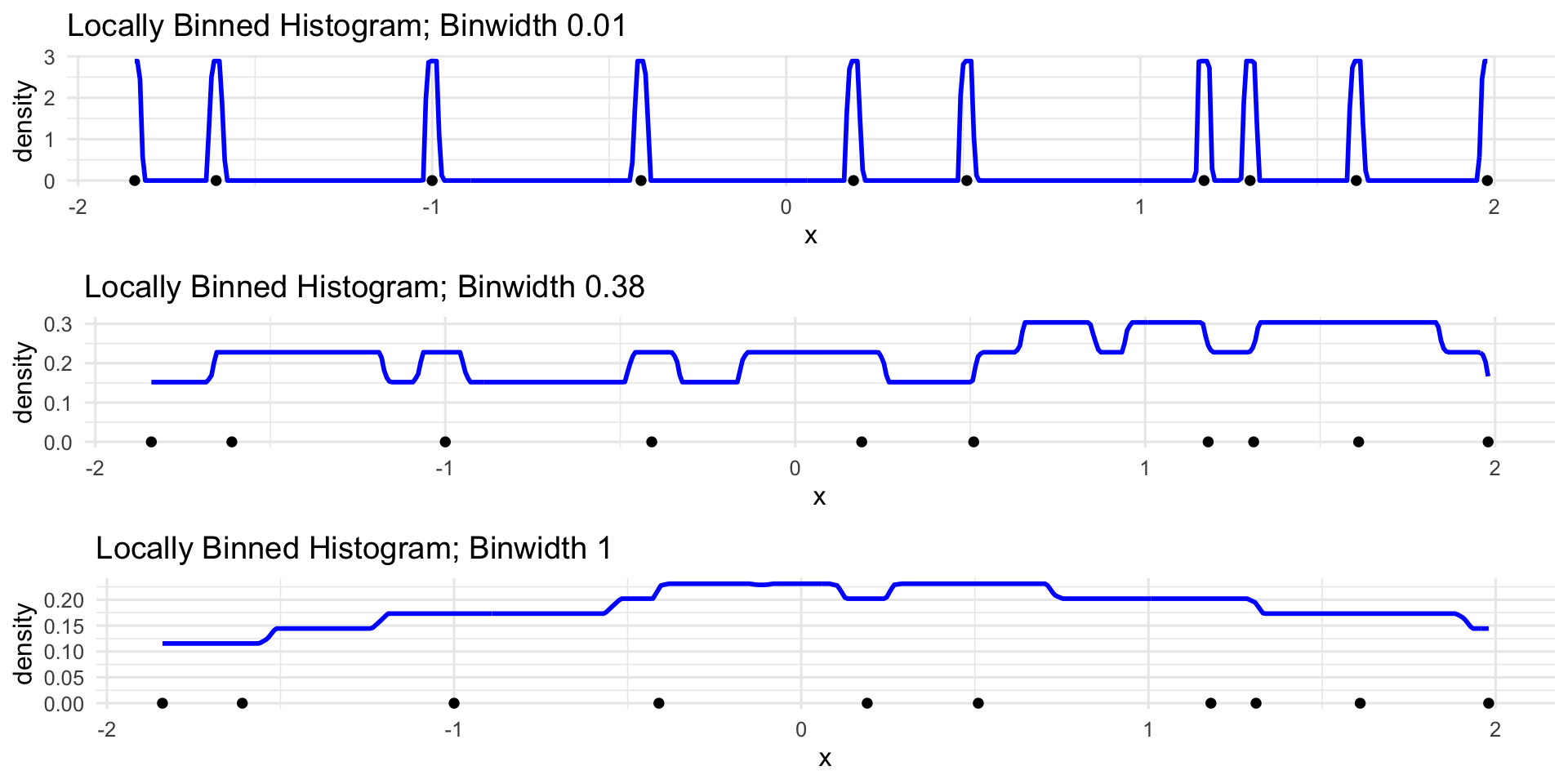
• This leads us to the idea of local binning, in which we allow the height at x to be a normalization of the count in a neighborhood of x of width h (as opposed to the count in one of a set of fixed bins).

Histograms, Revisited

Local Binning

\[ \widehat{f}_{\mathrm{lb}}(x) = \frac{1}{nh} \sum_{i=1}^{n} 1 \! \! 1_{\{ \left| x_i - x \right| < \frac{h}{2} \}} \]

Histograms, Revisited

Local Binning

Histograms, Revisited

Local Binning

\[ \widehat{f}_{\mathrm{lb}}(x) = \frac{1}{n} \sum_{i=1}^{n} \left[ \frac{1}{h} 1 \! \! 1_{\{ \left| x_i - x \right| < \frac{h}{2} \}} \right] \]

• Changing x_i amounts to changing the “center” of the “box”
• Changing h amounts to changing the width and height of the “box”
• Note, however, that for any value of h and x_i, the area underneath this graph is always 1.

• Nonnegative function that integrates to one…

Leadup

\[ \widehat{f}_{\mathrm{KDE}}(x) = \frac{1}{n} \sum_{i=1}^{n} \frac{1}{\lambda} K_{\lambda}(x, x_i) \]

• In this context, the function K(x, x_i) is referred to as a kernel function, provided it is nonnegative and integrates to unity: \[ \int_{-\infty}^{\infty} K_{\lambda}(x, x_i) \ \mathrm{d}x = 1, \ \forall x_i \]
  • Some people relax the condition of integrating to unity, but we’ll include it.
• So, again, what kinds of functions does this sound like?

Kernel Density Estimation

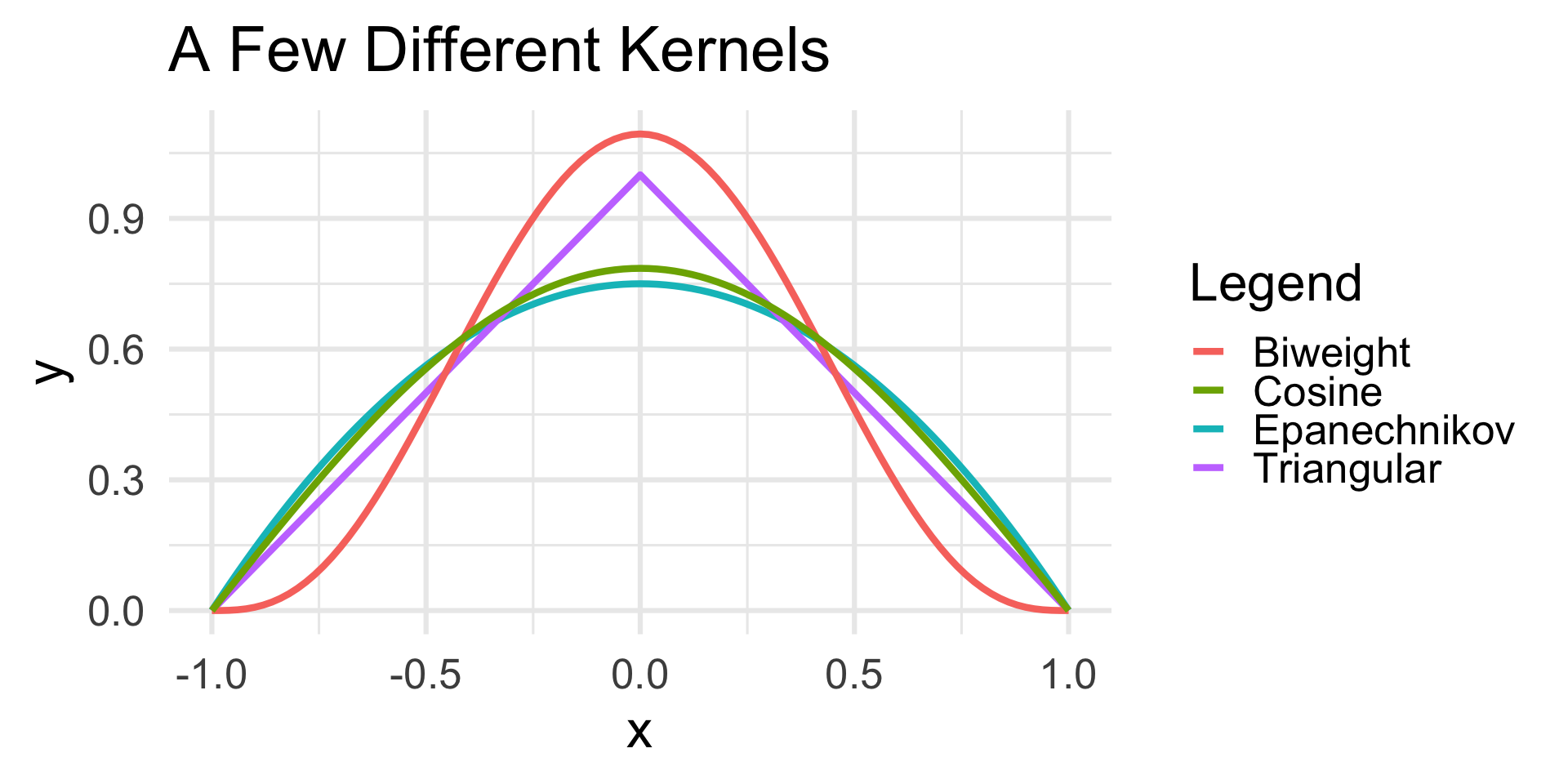
• In general, we can use any valid probability density function as a kernel.

• The estimate defined on the previous slide is called a kernel density estimate (KDE), and the general procedure of estimating a density as a weighted local average (with weights given by a kernel) of counts is called kernel density estimation.

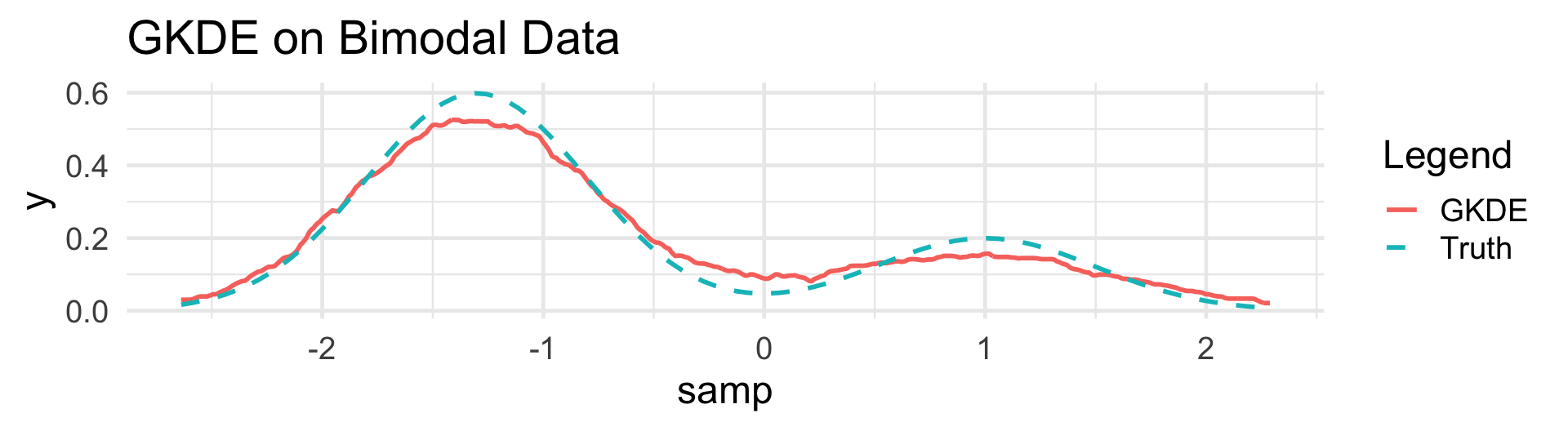
• Gaussian KDE utilizes a Gaussian kernel:

\[ \widehat{f}_{\mathrm{GKDE}}(x) = \frac{1}{n} \sum_{i=1}^{n} \frac{1}{\lambda} \phi\left( \frac{x_i - x}{\lambda} \right) \]

• Other kernels include the boxcar (equivalent to a locally binned histogram!), triangular, Epanechnikov (quadratic), Biweight (quartic), and a few others

Kernel Density Estimation

Kernels

density(...)        ## for analysis only
stat_density(...)   ## for plotting

 kernel = c("gaussian", "epanechnikov", "rectangular",
                   "triangular", "biweight", "cosine", "optcosine"),

Parametric Modeling: An Introduction

Parametric Modeling

• Recall that, in the parametric setting of modeling, we express our model in terms of a series of estimable parameters.

• For example, suppose we assume the weight Y_i of a randomly-selected cat to follow a Normal distribution with mean µ and variance 1, independently across observations.

Y_i \(\stackrel{\mathrm{i.i.d.}}{\sim}\) N (µ, 1)

Y_i = µ + ε_i, for ε_i \(\stackrel{\mathrm{i.i.d.}}{\sim}\) N (0, 1)

• Fitting a model to our data is therefore equivalent to finding the “optimal” estimates for the parameters in our model (in this case, µ).

The Modeling Process

More About Step 2

• This is precisely what is meant by Step 2 of the modeling procedure (sometimes called the model fitting stage): we identify estimators/estimates of the parameters that are ideal in some way.

• In our coin tossing example, our choice of estimation was relatively straightforward: use the sample proportion as an estimator for the population proportion.

• In many cases, however, there won’t necessarily be one obvious choice for parameter estimates.

  • For example, in our cat-weight example: do we use the sample mean or the sample median?
  • To estimate spread, should we use the mean or the median? Standard deviation or IQR?

Loss Functions

• In general, we can think of an estimator as a rule.

  • Mathematically, rules are functions - so, an estimator based on a single random observation Y can be expressed as δ(Y)

• A loss function is a mathematical quantification of the consequence paid in estimating a parameter θ by an estimator δ(Y).

  • More concretely, a loss function is a function \(\mathcal{L}: \R^2 \to \R^{+}\), where \(\mathcal{L}(\theta, \delta(Y))\) represents how poorly \(\delta(Y)\) is doing at estimating \(\theta\).

• The risk is the average loss: \(\mathbb{E}_{Y}[\mathcal{L}(\theta, \delta(Y))]\).

• An “optimal” estimator for θ is therefore one that minimizes the risk: \[ \widehat{\theta} := \argmin_{\theta} \left\{ \mathbb{E}_{Y}[\mathcal{L}(\theta, \delta(Y))] \right\} \]

Loss Functions

Illustration

• As an illustration of this framework of estimation, let’s attempt to find the value c that “best” summarizes a set of observations (y₁, …, y_n).

• As the distribution of Y is, in general, unknown, we can consider the empirical risk in place of the risk: \[ R(\theta) := \frac{1}{n} \sum_{i=1}^{n} \mathcal{L}(y_i, c) \]

  • Here, \(\mathcal{L}(y_i, c)\) can be interpreted as “how far away c is from y_i”.

• Again, our “best” summary will be the value of c that minimizes R(θ)

Loss Functions

• There are many choices for loss functions, each with pros and cons.

• For numerical data, the two most common loss functions are:

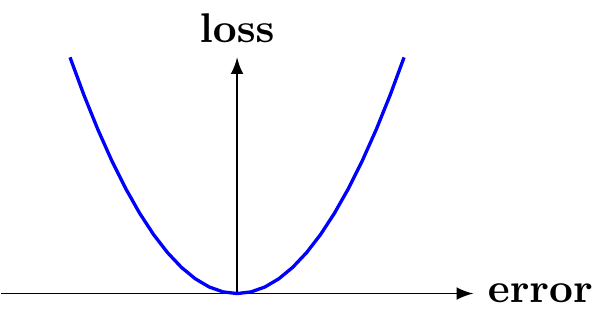
Squared Error (aka L₂)
\(\mathcal{L}(y_i, \theta) = (y_i - \theta)^2\)

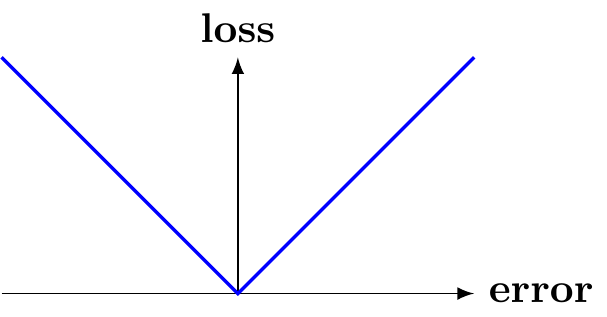
Absolute Error (aka L₁)
\(\mathcal{L}(y_i, \theta) = |y_i - \theta|\)

Loss Functions

• L₁ loss tends to be more robust to outliers than L₂ loss.

  • Keep in mind that, depending on the context, this could be a good or bad thing.
  • In general, it is up to you (the modeler) to decide which loss function to adopt.

• As an example of how loss functions help us construct estimators for parameters, let us consider the case of L₂ loss.

• Given data (y₁, …, y_n), our “optimal” (risk-minimizing) estimate for θ (under L₂ loss) satisfies \[ \widehat{\theta}_n := \argmin_{\theta} \left\{ \frac{1}{n} \sum_{i=1}^{n} (y_i - \theta)^2 \right\} \]

Loss Functions

Example: L₂-minimizing Estimate

• To optimize a function, we differentiate and set equal to zero:

\[\begin{align*} \frac{\partial}{\partial \theta} R(\theta) & = \frac{\partial}{\partial \theta} \left[ \frac{1}{n} \sum_{i=1}^{n} (y_i - \theta)^2 \right] \\ & = \frac{2}{n} \sum_{i=1}^{n} (\theta - y_i) = \frac{2}{n} \left[ n \theta - n \overline{y}_n \right] = 2(\theta - \overline{y}_n) \\ \implies 2(\widehat{\theta} - \overline{y}_n) & = 0 \ \implies \ \boxed{\widehat{\theta} = \overline{y}_n} \end{align*}\]

• So, the sample mean minimizes the risk under L₂ loss; i.e. if we adopt L₂ loss, then the value of θ that best fits the data is the sample mean.

Chalkboard Example

Chalkboard Example

Identify the summary statistic that minimizes the empirical risk under L₁ loss.

Modeling with Two Variables

Two Variables

• Both of our examples up until now can be classified as “univariate” modeling, as they involve only one variable.

• In data science, we are often interested in how two (or more) variables are related to one another.

• As an example, it’s not difficult to surmise that houses built in different years sell for different prices.

• As such, we can explore a dataset that tracks the median selling price of homes built in various years, as sold in King County (Washington State) between May 2014 and May 2015.

  • E.g. one datapoint represents the median selling price of a home built in 1963, sold in 2014.
  • Data Source, though we’re using a version that I aggregated and cleaned.

Housing Data

An Example

housing %>% ggplot(aes(x = yr_built,
                       y = avg_price)) +
  geom_point(size = 3) + 
  ggtitle("Median Selling Prices in 2014") +
  xlab("Year Built") + ylab("Median Selling Price") +
  theme_minimal(base_size = 18)

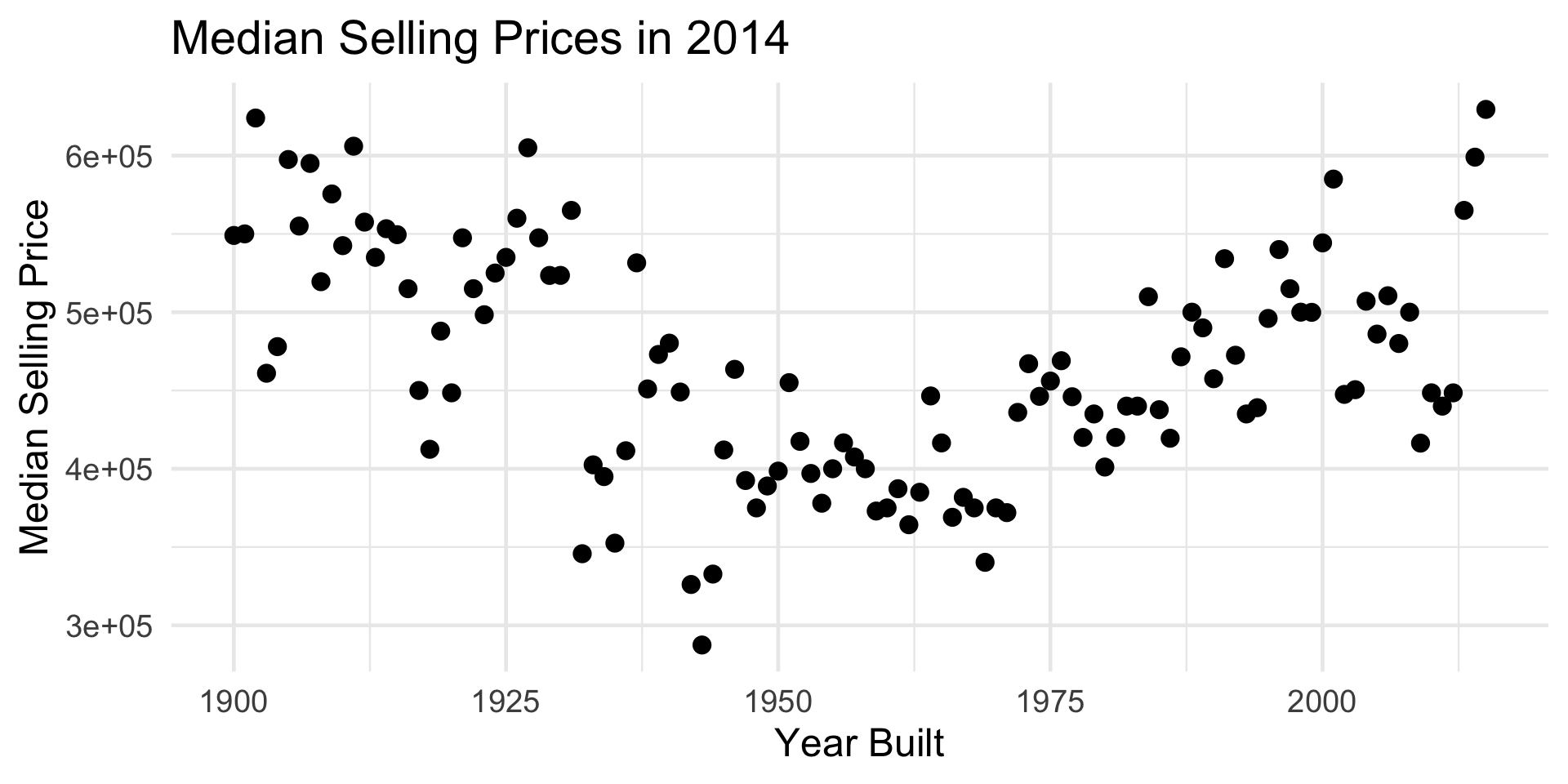
Housing Data

An Example

• Thinking back to the first week of this class:
  • Is there a trend?
  • If so, is the trend linear or nonlinear?
  • Can the trend be classified as positive or negative?
• Additionally, can anyone propose an explanation for the “dip” in prices near the middle of the graph?

Housing Data

Building a Model

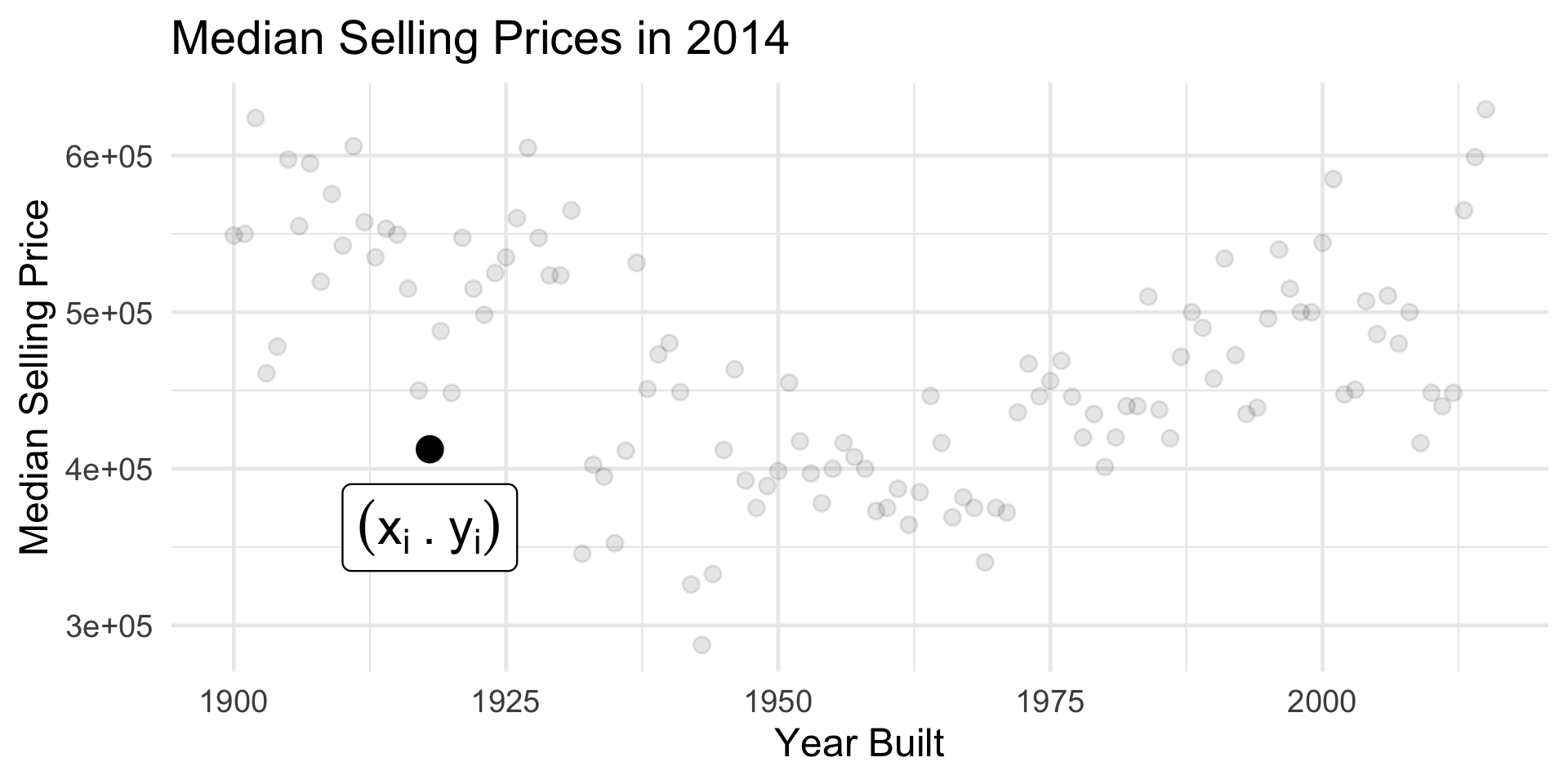
Housing Data

Building a Model

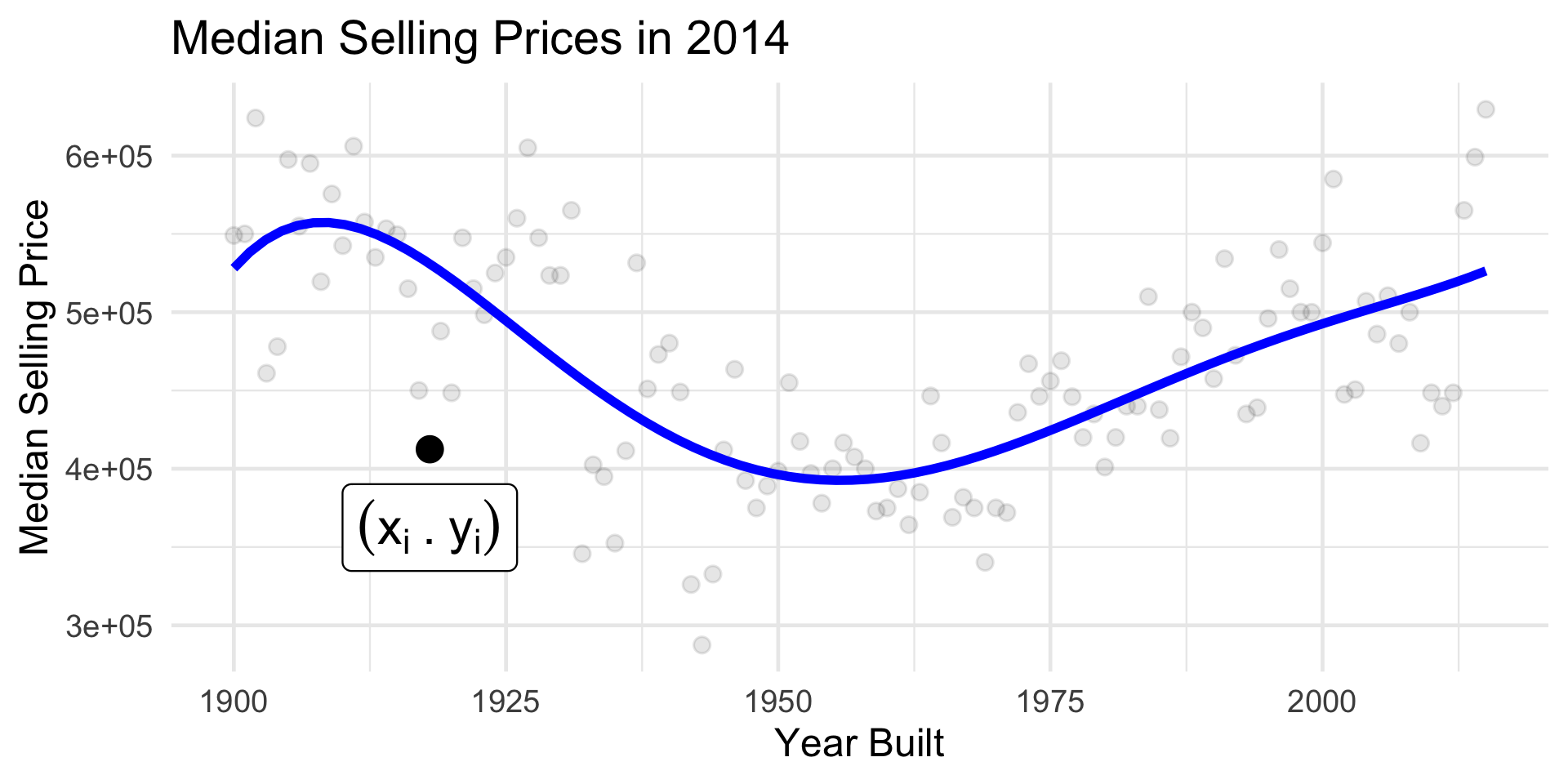
Housing Data

Building a Model

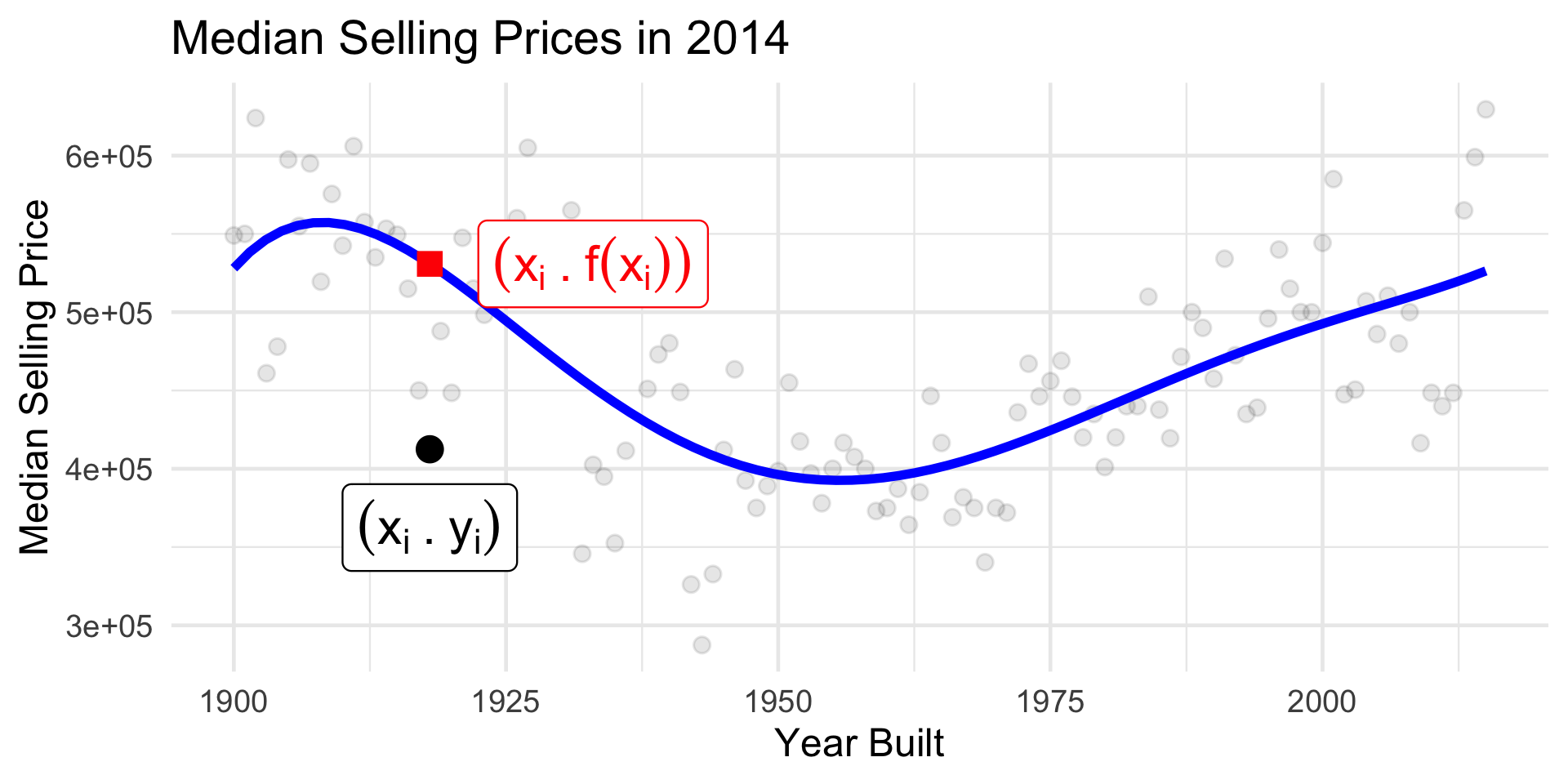
Housing Data

Building a Model

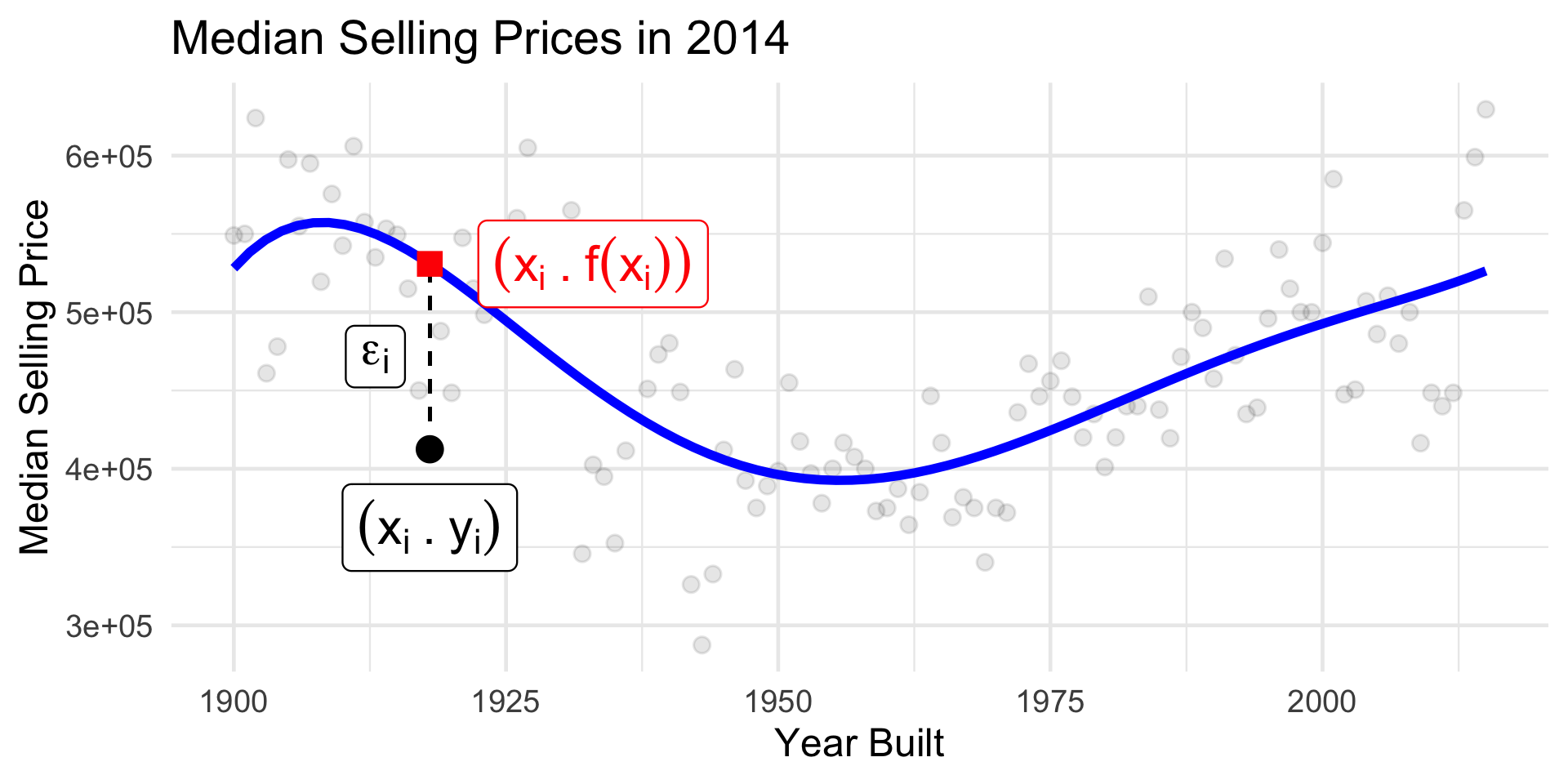
Housing Data

Building a Model

• In other words: for every year x_i we believe there is an associated “true” median selling price f(x_i).

• This true price is unobserved; what we actually observe is a median selling price y_i that has been contaminated by some noise ε_i.

  • This noise could be due any number of factors: measurement error, random fluctuations in the market, etc.
  • We’ll talk about this noise process more in a bit.

• Mathematically: \(y_i = f(x_i) + \varepsilon_i\), for some zero-mean constant-variance random variable ε_i.

  • It is precisely this error term that makes our model stochastic.

Statistical Models

Terminology

y = f ( x ) + noise

y: response variable

• Dependent variable
• Outcome
• Output

f: signal function

• Mean function

x: explanatory variable

• Independent variable
• Feature
• Input
• Covariate

• If y is numerical, the model is called a regression model; if y is categorical, the model is called a classification model.

Statistical Models

Noise

• The noise term can be thought of as a catch-all for any uncertainty present in our model.

• Broadly speaking, uncertainty can be classified as either epistemic (aka “reducible”) or aleatoric (aka “irreducible”).

• Epistemic uncertainty stems from a lack of knowledge about the world; with additional information, it could be reduced.

• Aleatoric uncertainty, on the other hand, stems from randomness inherent in the world; no amount of additional information can reduce it.

Statistical Models

Noise

• As an example: errors arising from a misspecified model are epistemic, as, in theory, if the model were corrected, they would be eliminated.

• On the other hand, measurement error is widely accepted as aleatoric; repeated measurements will not reduce the amount of measurement error.

• Since the noise term in our model captures the uncertainty present, we treat it as a zero-mean random variable.

• Later, we’ll need to add some additional specificity to this (e.g. what distribution does it follow? What assumptions do we need to make about its variance?) - for now, we’ll leave things fairly general.

Why Model?

Prediction

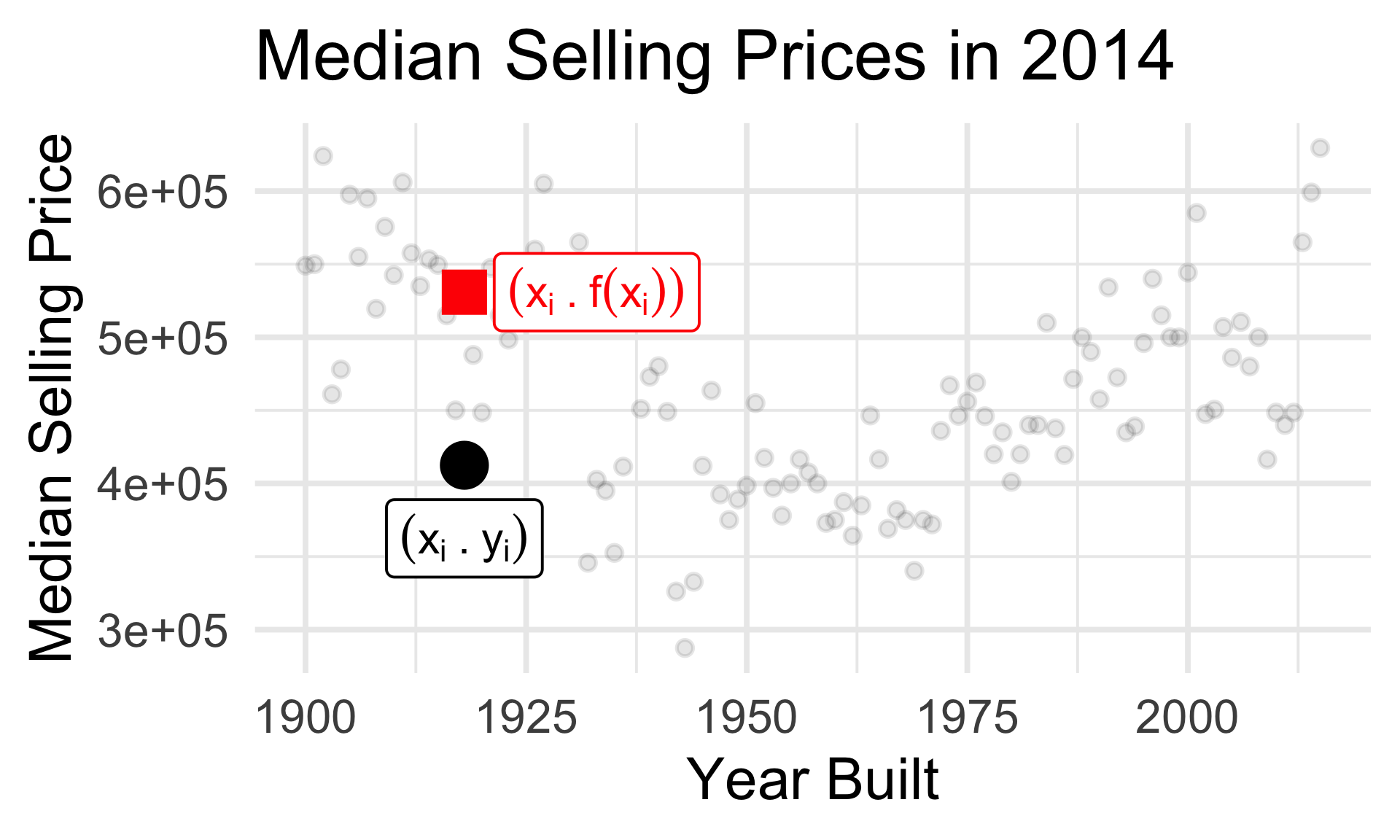
• What’s the true (de-noised) median selling price of a house built in 1918?

Inference

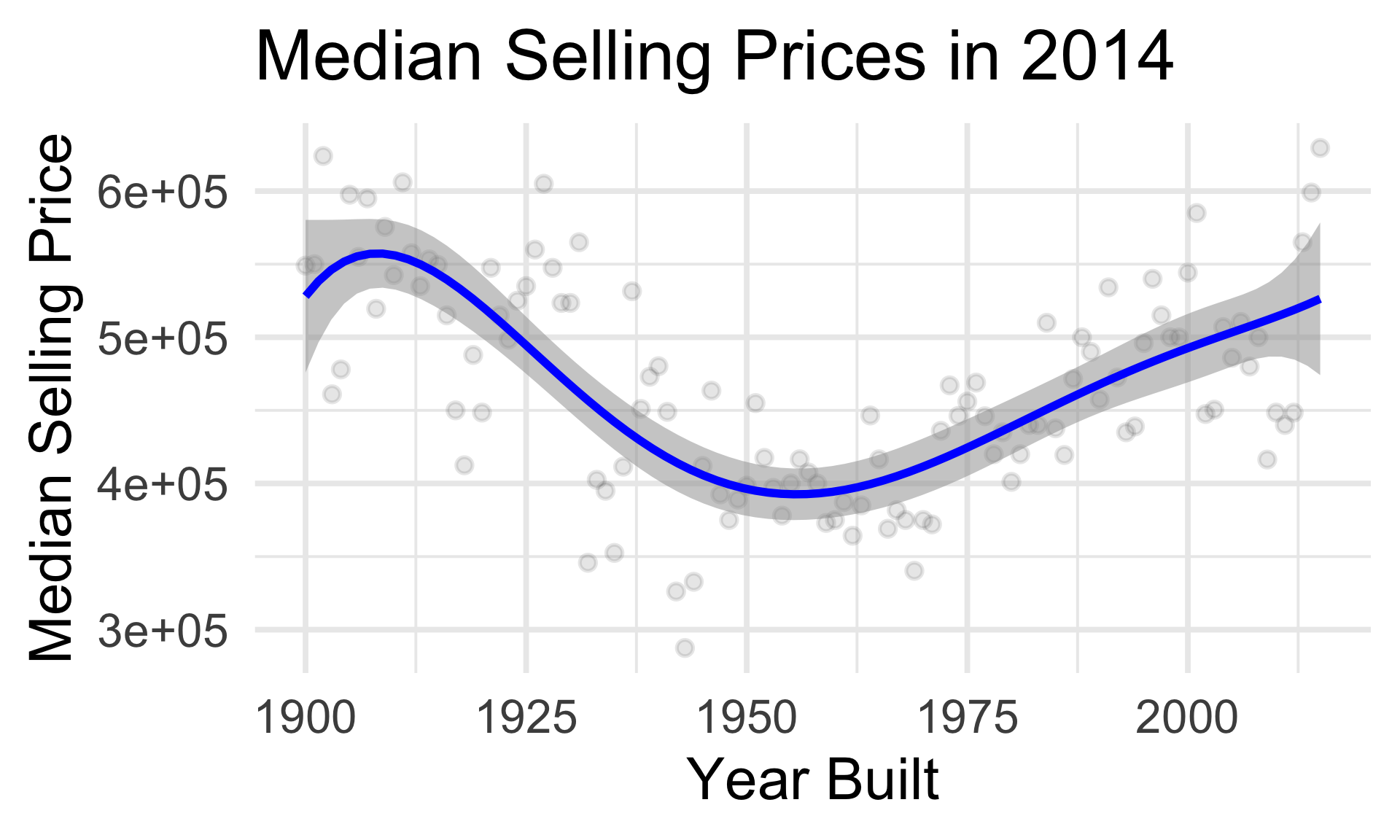
• How confident are we in our guess about the relationship between year built and selling price?

Next Time

• Tomorrow, we’ll start our discussion on a specific type of parametric model that lends itself nicely to analysis (called the SLR model).
  • Our discussion on the SLR model will last several lectures.
• REMINDER: Homework 2 is due This Sunday (July 20) by 11:59pm on Gradescope.